Faut-il connaître ces tables « par cœur » ? « Psittacisme » nous répète-t-on à l’envi, « on n’a pas besoin de connaître ses tables de multiplication pour être un bon mathématicien » nous assène Cédric Villani (en ajoutant aussitôt de manière paradoxale : « l’important c’est réfléchir vite, réfléchir en réaction, se demander quel est le sens de ces opérations ») autant de mauvais prétextes pour dégager parents et enseignants de ce qui leur apparaît le plus souvent comme une corvée : la mémorisation des tables.
Mais la mémorisation des tables n’a pas pour unique but de psalmodier une série de résultats qui fleurent bon la craie et le tableau noir, c’est aussi un outil pour « réfléchir vite » et «comprendre le sens de l’opération» . La construction des tables de multiplication et leur mémorisation doit faire appel à des méthodes qui ne se réduisent pas à un enregistrement mécanique mais ouvrent la voie à des notions plus complexes : sens de la division, proportionnalité, changement d’unité, conversion, fractions … Ces méthodes s’inscrivent dans le triptyque « manipuler, verbaliser, abstraire » (préconisé par mission Torossian Villani), énoncé autrefois de manière plus basique : « faire, dire, écrire ».
En CP, les premières manipulations pour introduire l’apprentissage des tables passeront par le boulier : le comptage de 2 en 2, de 3 en 3 … imprimera la comptine des résultats.
Le déplacement des boules sera d’abord associé au comptage, l’énonciation des nombres : 4, 8, 12, 16, 20 … ponctuera le déplacement des boules par quatre, puis, l’aisance aidant, on ajoutera les opérations : « 4 et 4, 8 ; 8 et 4, 12 ; 12 et 4, 16 … » pour commencer et, par la suite, le passage de l’addition répétée à la multiplication s’effectuera avec le changement de formulation : « 1 fois 4, 4 ; 2 fois 4, 8 ; 3 fois 4, 12 … ».
La manipulation de monnaie fictive permet un changement d’unité qui favorise l’imprégnation du comptage par 2 et par 5 (combien de pièces de 2 € pour avoir 14 € ? Combien de billets de 5 € pour avoir 25 € ? …) mais aussi une bonne approche concrète de la division et de ses deux sens (combien de pièces de 2 € pour avoir 10 € ? Combien de billets de 5 € pour avoir 10 € ? Combien chacun aura-t-il si je partage 10 € entre 2 personnes ? entre 5 personnes ?).
Les activités de distribution (de cartes, de bûchettes, de jetons …) donnent une preuve « par le geste » que la recherche de la valeur d’une part et celle du nombre de parts correspondent bien à une même opération : quand on partage 24 cartes entre 3 joueurs par distribution, chacun en reçoit une quand on en retire 3 du paquet ; partager 24 en 3 revient donc à chercher combien de fois on peut retirer 3 de 24. La verbalisation consistera ici à associer les expressions « 24 partagé en 3 » « en 24 combien de fois 3 » « 24 divisé par 3 » pour parvenir à l’écriture unique « 24 : 3 »
Mais ce sont les réglettes Cuisenaire qui se prêtent le mieux à cet entraînement facilitant l’acquisition des résultats des tables.
Voici un exemple d’utilisation de ces réglettes en fin de CP ou CE1.
– Former une longueur de « 24 » avec les réglettes.![]()
(La manière la plus rapide est de prendre deux réglettes de « dix » et une de « quatre », mais d’autres solutions peuvent être proposées).
– Trouver toutes les manières possibles de former cette longueur de 24 avec des réglettes d’une même couleur.
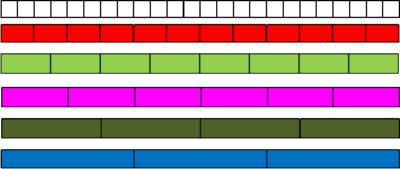
À partir du moment où les élèves ont trouvé toutes ces combinaisons, il importe de les amener à verbaliser les résultats obtenus en multipliant les questions. Par exemple, pour la dernière ligne :
– Quelle longueur donnent trois baguettes bleues ? Trois fois huit ? Quel est le triple de huit ?
– Combien de réglettes bleues pour avoir 24 ? En 24 combien de fois 8 ? 24 partagé en 3 ? 24 divisé par 3 ? Quel est le tiers de 24 ?
Dans un premier temps, on peut juste demander de montrer la réglette ou la ligne demandée, mais il est important d’exiger ensuite une phrase réponse complète qui reprend la formulation choisie dans la question.
Quand l’exercice est bien rôdé, on peut passer aux divisions avec reste :
– Combien de réglettes de cinq pour faire 24 ? Qu’est-ce qui manque ? … En 24 combien de fois 5 ? et il reste ?
Et même aux additions et soustractions de fractions :
– Combien font deux tiers de 24 ? Combien reste-t-il si on retire un tiers à 24 ?
Si l’exercice commence par la manipulation, il peut se poursuivre uniquement avec le regard, sans toucher aux réglettes et laisser aussi une place à l’estimation : « En 24 combien de fois 7 ? que restera-t-il ? » avec une vérification a postériori. On peut même travailler au toucher, les yeux bandés, avant d’aborder la mémorisation, sans supports matériels.
On insiste trop souvent sur le côté ludique de la manipulation, l’objectif visé ici est l’automatisation des calculs de base, c’est l’aisance dans ces calculs qui sera source de satisfaction, pas le fait de jouer avec des objets. Aussi ce type d’exercice trouvera-t-il encore sa place au CM quand on abordera le travail sur les fractions.
Beaucoup estiment que l’important n’est pas de connaître les tables de multiplication mais de savoir les reconstruire. Après des années d’abandon de la pratique de la multiplication et de la division au CP, il n’est pas rare de voir des élèves qui trouvent le résultat de trois fois huit en ajoutant mentalement 8 + 8 + 8. Ils ont compris le sens de l’opération et peuvent trouver le bon résultat, s’ils ont acquis une bonne pratique du calcul additif. Mais quel temps et quelle énergie gaspillés par rapport à celui qui peut répondre du tac au tac : « 24 ! ».
Faut-il alors s’étonner des difficultés rencontrées par des élèves de collège trop souvent incapables de résoudre correctement une division posée et de maîtriser le calcul de fractions ?
Pascal Dupré
Un exemple de progression de cet apprentissage au CE1 : Le manuel COMPTER CALCULER CE1
